Submanifold Convolution [part 1] - Introduction

This is the first part of my ? part series on the implementation of submanifold convolution. This part will provide a high-level overview for the implementation of submanifold convolution.

Submanifold Convolution

Submanifold convolution operates on a sparse input with -dimensional grid of sites. A site in the input is considered to be active if the feature vector associated with it is non-zero, otherwise it is considered to be inactive.

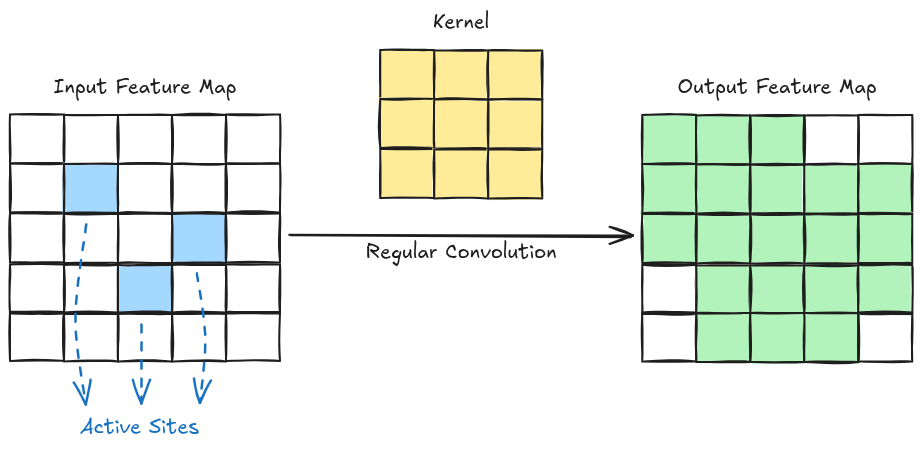
We can perform convolution by making a site in the output active if any of the inputs to its receptive field is active. However, this has the problem of dilating the set of active sites, i.e. it doesn’t preserve sparsity, as shown below:

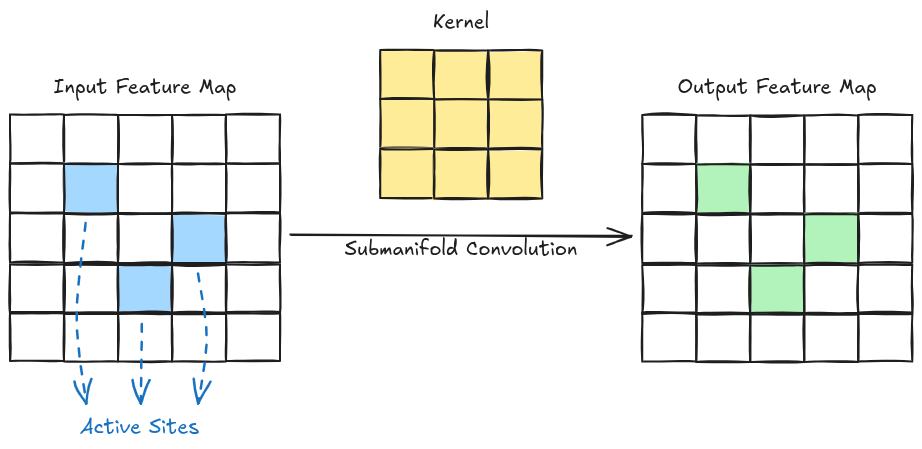
This problem can be solved by making a site in the output active by only considering the central active input to the receptive field. This type of convolution is called Submanifold Convolution. The output set of active sites in such a convolution exactly mirrors that of the input set as shown below:

Sparse Tensor

Before we delve into the implementation overview, let us look at the representation of a sparse feature map as a sparse tensor:

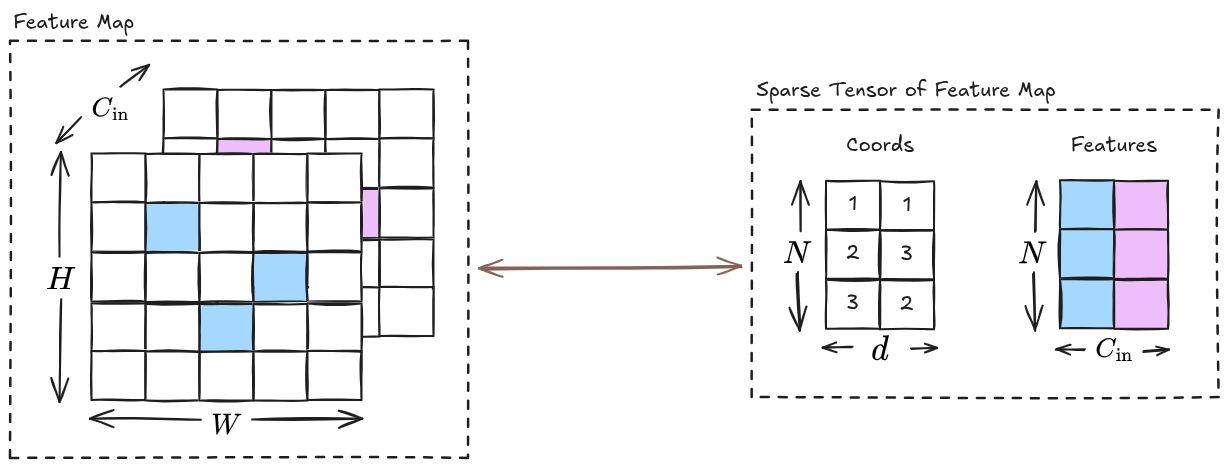
The sparse tensor representation of the feature map has:

1. A coords tensor of the active sites in the original feature map. Here, is the number of active sites, and is the number of spatial dimension in the original feature map. In our above example, and for width and height .
2. A features tensor consisting of feature vectors corresponding to the coords. Here, is the number of input channels, which is in our above example.

Although not shown in the above example, the sparse tensor representation also consists of information related to the shape of the original feature map.

Implementation

To implement submanifold convolution efficiently, we need a way to fetch the neighbors of the active sites. For this purpose, we do the following two things:

1. Create a hash map that maps each index in the coords to the index in the flattened original feature map. (This will be explained in part 2)
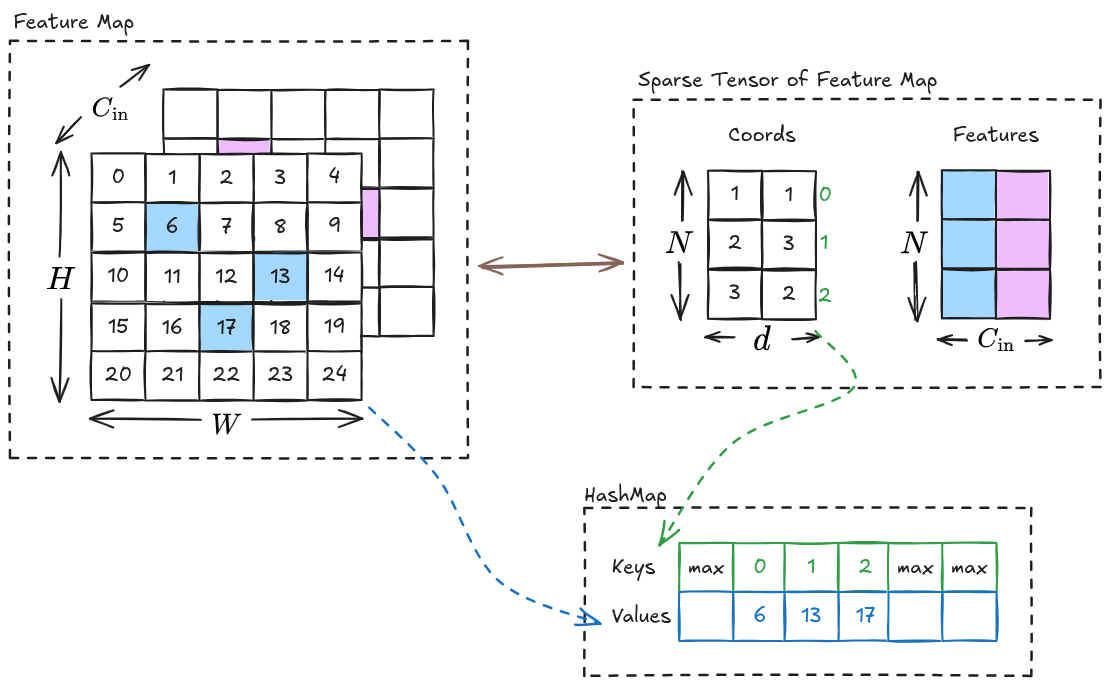
2. Use the hash map to create a neighbor map. For each active sites, the neighbor map contains the location of its active neighbors. (This will be explained in part 3)

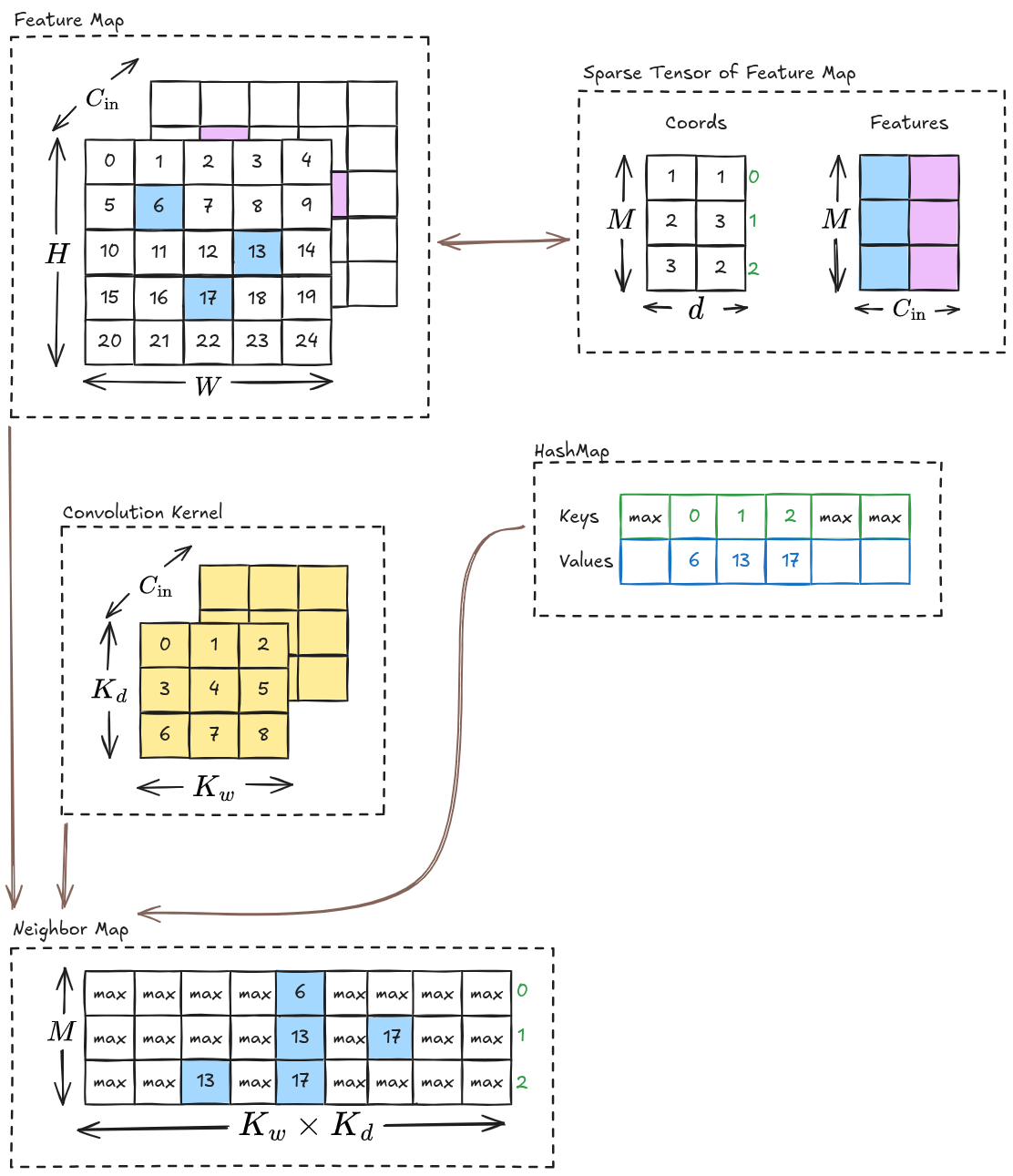
Once we have a way to fetch the neighbors, we can apply the convolution algorithm to obtain the result. We will be looking into the following convolution algorithms:

1. Explicit GEMM
2. Implicit GEMM
3. Implicit GEMM Split-k
4. Masked Implicit GEMM
5. Masked Implicit GEMM Split-k

References

• Submanifold Sparse Convolutional Networks
• FlexGEMM: A Cross-Platform Backend for High-Performance Sparse Convolutions